【ポケモンコロシアム】スナッチリストを開いた時の消費について【乱数調整】
この記事はPokémon RNG Advent Calendar 2020 9日目の記事です。

かけらさんの調べたもののまとめ記事に以下のような記述があります。
ここで注意なのですが、なぜかここで生成されるポケモンにはID0(TID&SID=0)で色回避ルーチンが作動します。ごくまれに7消費ではなく9消費になってしまう。とても低い確率なので気にする必要はないと思いますが、よく分からないずれが起きたらこいつのせいかもしれません。
この事象がどのくらいの確率で発生するのか実際に調べてみました。
使用したコードは以下の通り。
int cnt = 0;
for(uint upper=0; upper<0x10000; upper++)
{
for(uint lower=0; lower<0x10000; lower++)
{
var seed = (upper << 16) | lower;
if ((seed.GetRand() ^ upper) < 8) cnt++;
}
}
Console.WriteLine(cnt);
Console.WriteLine(cnt / (float)0x100000000);
実行結果は以下の通り。
524348 0.0001220843
該当するseedが大体52.4万個くらい存在して、適当にスナッチリストを開いたときに引いてしまう確率は0.012%くらいですね。確かに気にしなくていいくらいの確率です。 とは言うものの、乱数調整は『確率的に動いていると見なされている事象を決定論的なステージに引き下ろす行為』なので、実際に気にするべきは単なる確率ではなく『理想個体を生成するseedの十分近くで、しかも7n消費手前に存在するようなseedの中に、このようなseedが存在するかどうか』でしょう。
以上、おまけのコーナーでした。
【ポケモンコロシアム】瞬きを用いた現在seed特定処理の実装と高速化【乱数調整】
この記事はPokémon RNG Advent Calendar 2020 23日目の記事です。

初めに
今年はポケモンコロシアム(2003年発売)の乱数調整にいくつもの大きな進展がありました。2月下旬にかけら(sina_poke)氏によってステータス画面におけるポケモンの瞬きを観測して現在seedを特定する手法が開拓され、スイクンを含む一部ポケモンの乱数調整の難易度が大きく緩和されたのをきっかけに、3月末にはライコウの乱数調整が可能になり(頑張りました)、現在ではフェナス/パイラ市中での戦闘になるポケモンを除いたほとんどのポケモンの乱数調整が現実的な難易度になっています。
今回はそんなブレイクスルーのきっかけとなった瞬きによるseed特定アルゴリズムの実装についての考察をまとめました。
瞬き処理の概要
瞬き発生の具体的な処理はかけらさんが公開されています。
ものすごく要約すると
ということです*1。この瞬きの間隔を十分多く観測すれば*2、現在seedを求めることができるというわけです。
動機
さて、この瞬きの観測ですが、人間がやるのはちょっと辛いです。主に目に優しくない。そこでPC上に映したGCの画面からテンプレートマッチングで瞬きを判定し、自動で瞬き間隔を収集するプログラム*3を書いたのですが、そこからseedの検索まで行ってくれた方が何かと嬉しいです。残念ながらかけらさんはCoToolに実装されている検索アルゴリズムまでは公開されていないので、自前でアルゴリズムを考察・実装する必要がありました。
考察
⓪要件
目視にしろプログラムによる自動観測にしろ、どうしても観測には誤差が生じます。そこで、ある程度の誤差を許した検索ができる必要があります。また、ポケモンコロシアムの主要な乱数消費手段はゲームロード後のダークポケモンのステータス画面を開いて放置することである都合上、検索範囲は数百万 ~ 数千万に及びます。*4
① ナイーブな実装
とりあえず考えられるのは『各seedから瞬きをシミュレートし、すべて入力から誤差以内になっているものを探す』です。
②『次に瞬きするまで』をあらかじめ計算しておく
①の実装の『瞬きするまで乱数を進める処理』は無駄があるように思えます。たとえばフレーム目からシミュレートを始めて、1回目の瞬きが
フレーム目、2回目の瞬きが
フレーム目だったという結果が得られたとしたら、次に
フレーム目からシミュレートを始めるときは先ほどの結果から、1回目の瞬きが
フレーム目に起こることはわかっています。しかしこの実装では同じ計算を再度行っているのです。
この発想をもう少し進めてみます。瞬きをシミュレートせずとも乱数値からただちに計算できることとして、『内部カウンタがいくつ以上なら瞬きが発生するか』があります。これを用いて『そのフレームで瞬きしたときに次に瞬きするのは何フレーム後か』を計算しておけば、シミュレート部分がかなり楽になります(これをa[n]で置いておきます)。
ここで『そのフレームで瞬きしたときに次に瞬きするのは何フレーム後か』を計算する部分ですが、『各iに対して、a[i+k]≦kを満たすような最小のkを、0から数え上げて探す方法』と、『各iに対して、i-85からi-a[i]で瞬きが発生していたらその次に瞬きが起こるのは少なくともiフレームの地点であることを利用する方法』があります。*5
上記の2つの方法ですが、今回は後者の方が効率的に計算することができます。それは瞬き判定の閾値が1/60で頭打ちになってしまうことに依ります。すなわち、与えられる疑似乱数は59/60の確率で『前回瞬きしてから90F経過していないと瞬きが発生しない乱数』なのです。つまり、前者の処理を行えば59/60の確率でループを86回回す羽目になりますが、後者の処理では59/60の確率でループが1回で済みます。
以上の発想で実装したのが以下のコードです。
③配列上の探索処理の効率化
これはかなりのガバなのですが、FindIndexは線形探索をしているので死ぬほど遅いです。しかも上記の通り、ほとんどのseedは最後尾まで探索しないと条件を満たさないので、処理効率的には最悪です。素直に二分探索しましょう。*6 処理回数が数百万回 ~ 数千万回に及ぶので、かなりの時間短縮が期待できます。*7
④配列上の探索処理をもっと効率化
乱数の取り得る値は65536通りしかないので、各0から65535の値に対してあらかじめUpperBoundしておいた結果を配列にキャッシュしておくことで、『そのフレームで瞬きしたときに次に瞬きするのは何フレーム後か』は配列へのアクセスだけで(つまり計算量で)取得できるようになります。
現在私がGithubで公開している、ポケモンコロシアムの乱数調整汎用ライブラリPokemonCoRNGLibraryに実装してあるのはこれになります。
実行時間の計測
実際に計測してみないことにはどれが優れているのか、どの程度優れているのかを比較して語ることはできません。以下のコードで計測してみました。*8
なおExectionTimer.MeasureはActionを渡して10回実行した平均時間を返す自前のメソッドです。
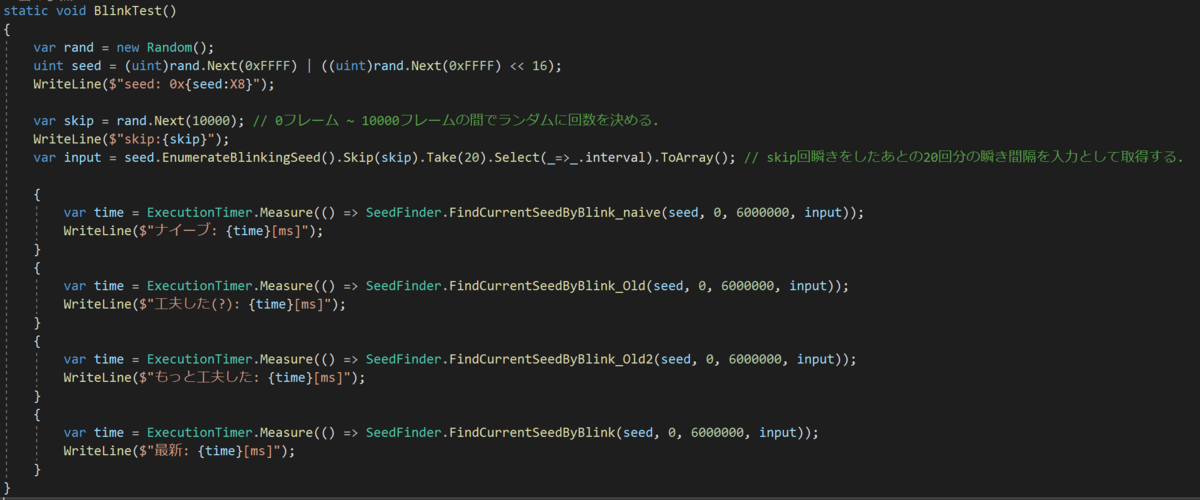
結果がこちら。
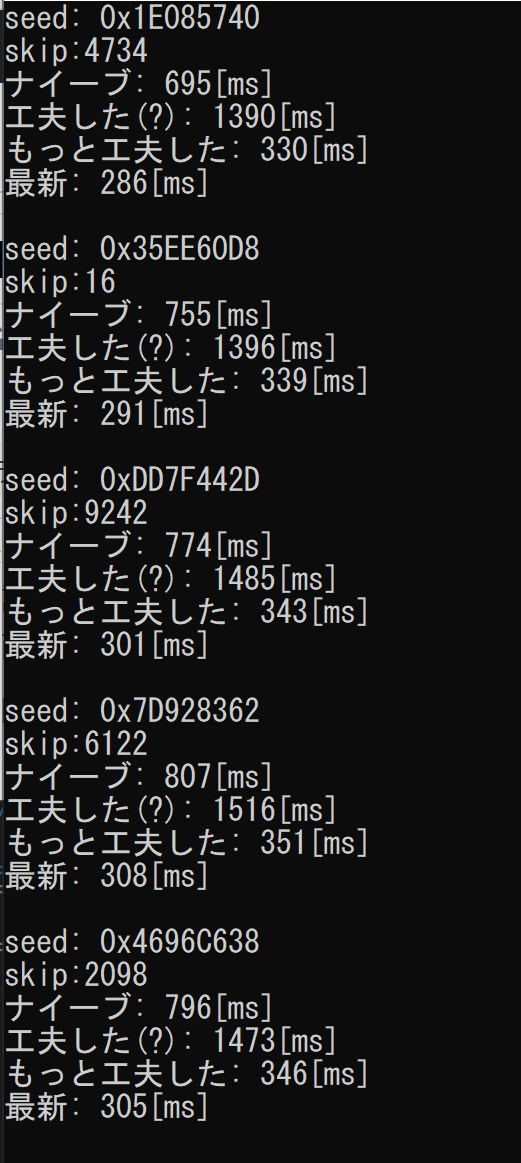
ナイーブな実装の2.5倍くらい速くなりました。やったー。そしてやっぱり②遅いですね……。上の画像は検索範囲を600万で取っていますが、1億くらい取っても④の実装なら5~6秒で計算が終わります。*9
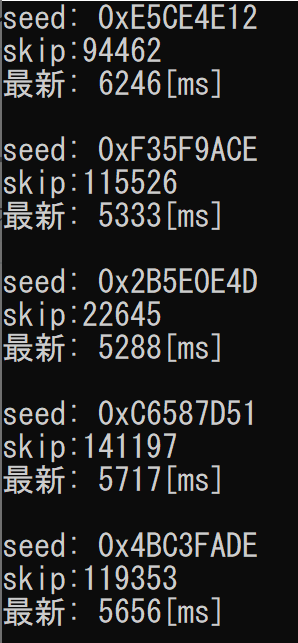
最後に
もっと良い実装があればライブラリにプルリク送ってください。待ってます。
あと良ければライブラリ使ってくださると嬉しいです。ほとんどの処理をイテレータで処理できるようにしてあるので、乱数ツールの肝になるリストの列挙等をほとんど脳死でコーディングできるようになっていると思います。
*1:厳密にはステータス画面に入った直後のみ、FPS変更のタイミングのせいか、2→5→7→…とカウンタが途中から奇数で動くのですが、誤差を考慮するならこれが大きく影響することはほとんどないでしょう
*2:これは厳密に証明したわけではなく経験則ですが、10~15回分ほどの瞬き間隔のデータが得られれば誤差±20でもほとんど一意的に現在seedが求まります
*3:COReaderという名前で公開しています。ただし2020/12/23現在公開しているバージョンの検索アルゴリズムは、ちゃんとテストしていなかったので、ナイーブな実装よりも遅いです
*4:あらかじめ消費速度をしっかり計測しておくことで、もっと細かく絞り込むこともできなくはないのですが、ざっくりした範囲指定で特定できるに越したことはありません。瞬きによるseed検索は検索範囲が広くても必要な入力数はほとんど変動しないのでなおさらです。
*5:いわゆる『貰うDP』と『配るDP』に似てるな~と思った。
*6:しかしC#のLinqにはBinarySearchしかなく、UpperBoundが無い(悲しい)。ここは自力で実装しました。
*7:あるいはかなりの無駄を生むカスコードを書いてしまったとも言えます
*8:コードブロックではなく画像なのは見たまま編集でここまで書いてしまったからです
*9:ただし要素数10^8の配列を作るのでメモリ使用量がえらいことになります。幸い範囲を適当に分割してやっても"被り"は入力の要素数*85程度しか発生しないので、適当に内部で分割してやってもいいかもしれません。要検討。
【ポケモン剣盾?】ハイドロポンプの略称を全部列挙する【プンポロドイハ】
諸悪の根源
『ポケットモンスター』縮めて、ポケモン#ハイドロポンプ 縮めて、ハイポン❓ドロポン❓ハインプ❓イドポプ❓ pic.twitter.com/emT4Gl3LVj
— 【公式】ポケモン情報局 (@poke_times) June 15, 2020
私はドロポン派です。
ポケモン公式が「ハイドロポンプの略称」という俗っぽい話題に言及したことで、Twitter各所でハイドロポンプの略称が話題に上がるようになりました。古来から各派閥に分かれて血を血で洗う争いが続いていたので、公式の爆弾投下によってTwitterが戦場にならないか心配ですね。ドロポン以外ならプンポロドイハが好きです。ドッヘンアイアも好きです。
そのような流れの中で、下のようなツイートを見かけました。
Q.ハイドロポンプの略し方、何通りあるか答えよ。ただし、略した名称は6文字以下とし、「ハイドロポンプ」は含まないものとする。
— @SUR(する) (@porigon865885) June 15, 2020
っていう数Ⅲの問題。
各文字を含めるか含めないかで考えれば=128、空文字と「ハイドロポンプ」は含めないので答えは128 - 2 = 126通りです。(数Aでは…?)
さて、これをもう少し改変して次のような問題を考えてみます。
「ハイドロポンプ」の1文字以上6文字以下の略称を「ハイドロポンプ」辞書順に全て列挙せよ。
— ARROWTUNA (@sub_827) June 15, 2020
ただし『略称』とは『ハイドロポンプ』の順序を保った部分文字列を指す。
定期テストで出てきたらめちゃくちゃ時間食われるのでスルー安定です…。
人力で126通り書き上げるのはとても大変ですが、コンピュータに任せればサクッとやってくれます。
……ホンマか?
言っておいて簡単じゃなかったら困るので自分で解いてみました。
できた pic.twitter.com/82p5lIck0O
— ARROWTUNA (@sub_827) June 15, 2020
(ちょっと難しかったです…)
「各文字について入れる/入れないで分岐して126通りの文字列を作った後ソートする」という方針だと「ソートする」の部分が少し厄介です。私は幅優先探索で解いてみました。
最後に
7文字入っちゃってるじゃん。
— ハャ卜(お父さん犬) (@PaintDoble) June 15, 2020
問題の条件には気を付けましょう。
追記
アイアンヘッドの略称の列挙は「ア」が2個含まれているので、もう少し難易度が上がります。誰か挑戦してみませんか?
追記2
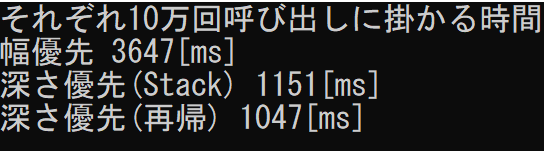
フォロワーさんから「再帰で書いた方が速かった」と刺されたので考え直してみましたが、深さ優先で解くべき問題でしたね。再帰ではなくStackを使って書いてみました。文字の追加の順番が逆になるので注意が必要です。
計測結果
TinyMTの更新を行列で書いてみようのコーナー(後編)
初めに
TinyMTの更新を行列で書いてみようのコーナー(前編) - yatsuna_827’s blogのつづき。 前編では数式が盛り沢山だったせいで多数の数学アレルギー患者に急性発作を引き起こさせてしまいましたが、今回は1と・しか出てこないので比較的安全だと思います。
前回求めた行列
$$
\begin{align}
\begin{bmatrix}
{\boldsymbol s}'_{0} & {\boldsymbol s}'_{1} & {\boldsymbol s}'_{2} & {\boldsymbol s}'_{3}
\end{bmatrix} =
\begin{bmatrix}
{\boldsymbol s}_{0} & {\boldsymbol s}_{1} & {\boldsymbol s}_{2} & {\boldsymbol s}_{3}
\end{bmatrix}
\begin{bmatrix}
{\boldsymbol O} & U_{31}C_{mat1} & U_{31}(L'_{1}L'_{10}+ C_{mat2}) & U_{31} L'_{1} \\
I & C_{mat1} & L'_{1}L'_{10} + C_{mat2} & L'_{1} \\
{\boldsymbol O} & I+C_{mat1} & L'_{1}L'_{10} + C_{mat2} & L'_{1} \\
{\boldsymbol O} & (I + R_{1})C_{mat1} & R'_{1}L_{10} + R'_{1}C_{mat2} & R'_{1}
\end{bmatrix}
\end{align}
$$
確認したところで、一列ずつ行きましょう。
1列目
零行列と単位行列
しか無いので特筆することは無いです。
見やすいように0は・で表します。零行列は全部・なので割愛。単位行列は

です。(こっちも言うまでも無いですが)
2列目
まず前編を書いた後で気づいたのですが、が成り立ちます。
は最下位bitのみに作用するので、最上位bitが欠落しようが何の関係も無いのです。なので、2列目の1行目と2行目はどちらも
です。
mat1は0x8f7011eeで、2進数に直すと10001111011100000001000111101110となります。はこれを最下段に並べた行列で、

となります。
はこれに単位行列を加えた行列で、

です。
そしては、
に
を加えた行列です。
は自信が無かったのでExcelくんに計算してもらいました。結果的には
を右と上にそれぞれ1ずつずらした行列です。
よって
は、

となります。
3列目
まずはを展開しましょう。
が成り立つので、括弧を展開すると
$$
\begin{align}
(I + L_{1})(I + L_{10}) &= I + L_{1} + L_{10} + L_{1}L_{10} \\
&= I + L_{1} + L_{10} + L_{11}
\end{align}
$$
となります。
ただし、4行目の
の展開は
は成り立たないので注意です。(押し出されたbitの情報が欠損するため。)
こちらは、
$$
\begin{align}
(I + R_{1})L_{10} = L_{10} + R_{1}L_{10}
\end{align}
$$
で終わりです。
また、に
を作用させると、自動的に最上位bitは押し出されて欠落するので、
$$
U_{31}L_{n}=L_{n}
$$
が成り立ちます。
以上を踏まえると、3列目は1行目から順に
$$
\begin{align}
U_{31} + L_{1} + L_{10} + L_{11} + C_{mat2} \\
I + L_{1} + L_{10} + L_{11} + C_{mat2} \\
I + L_{1} + L_{10} + L_{11} + C_{mat2} \\
L_{10} + R_{1}L_{10} + C_{mat2} + R_{1}C_{mat2}
\end{align}
$$
となります。
は

という行列で、mat2の値はmat2 0xfc78ff1f(2進数で11111100011110001111111100011111)なので、は

なので、1行目は

という行列になります。2行目、3行目はほぼ同じ行列で、(1,1)成分が1になっただけです。

4行目、は

です。よく見るとと
とは若干異なっているのがわかると思います。
は

なので、4行目は

となります。
4列目
ほとんどまんまです。1行目は
$$
U_{31}(I + L_{1}) = U_{31} + L_{1}
$$
なので、

2行目、3行目はで、

4行目はで、

です。
組み合わせる
これらの行列を並べると、前回求めた更新を表す行列ができあがります。

ワッショイ!
最後に
計算が苦手なので大変でした(小並感)。ですが、Excelを使うことで、計算が合っているかどうかを確かめながら作業を進めることができました。
線形代数の初めの方に出てくるクッソめんどくさい行列計算は、Excelを使うととても楽です。逆行列も求められます。ということで…
オマケ
最後の最後に
前編を書き上げた後で計算ミスやら記述ミスやらが次々発覚してサイレント修正しながら後編を書きました。大晦日に。ガキ使見ながら。弟たちは友達の家に遊びに行っているというのに。。。
それは置いておくとして、本家MTも同様に624項をまとめて1つの内部状態とみなすことで、行列を用いて
と表せるので、誰かやってみてください。求める過程自体は、おそらくTinyMTよりも簡単だと思います。来年のAdvent Calenderのネタにどうでしょうか。
それではよいお年を。
TinyMTの更新を行列で書いてみようのコーナー(前編)
はじめに
この記事はPokémon RNG Advent Calendar 2017 21日目の記事です。
21日の枠が空いていたので、怖い人に脅されて急遽昔やったネタを引っ張り出してきました。
これ。
twitter.comTinyMTの更新関数(遷移関数)を行列で表してみました(MAT等の値はポケモンSMで使われている値)。 状態空間(status[0]~[3])を1本の横ベクトルで表すと、更新関数f(x)はこの行列Aを用いて「f(x) = xA」と表せます。 見やすいよう1のセルを黒くしました。 pic.twitter.com/e32oMSDOkb
— 夜綱 (@sub_827) 2017年3月30日
さっさと書き上げるはずだったのですが、なんと計算したメモがロクに読めたもんじゃないという事態が発生し、一から計算し直す羽目に。
その結果クリスマスはルーズリーフと格闘して過ごしました。どうにも計画性が無さすぎて困る。
というわけで、一気に書き上げる気力が残っていないので、前後編に分かれます。
本題
去年のAdvent Calenderではおだんぽよ氏が行列を用いてTinyMTの逆算処理を求めていましたが、 この記事ではその行列を具体的に求めていきたいと思います。
更新処理の確認
まずはTinyMTの更新処理のソースコードを見てみましょう。
inline static void tinymt32_next_state(tinymt32_t * random) {
uint32_t x;
uint32_t y;
y = random->status[3];
x = (random->status[0] & TINYMT32_MASK)
^ random->status[1]
^ random->status[2];
x ^= (x << TINYMT32_SH0);
y ^= (y >> TINYMT32_SH0) ^ x;
random->status[0] = random->status[1];
random->status[1] = random->status[2];
random->status[2] = x ^ (y << TINYMT32_SH1);
random->status[3] = y;
random->status[1] ^= -((int32_t)(y & 1)) & random->mat1;
random->status[2] ^= -((int32_t)(y & 1)) & random->mat2;
}
https://github.com/MersenneTwister-Lab/TinyMTより
これを、random->status[n] = s[n]と置いたり、定数に具体的な値を入れたりして、もうちょっと読みやすく書き直すと以下のようになります。
y = s[3];
x = (s[0] & 0x7FFFFFFF) ^ s[1] ^ s[2];
x ^= (x << 1);
y ^= (y >> 1) ^ x;
s'[0] = s[1];
s'[1] = s[2];
s'[2] = x ^ (y << 10);
s'[3] = y;
if(y&1==1){
s'[1] ^= mat1 // 0x8f7011eeだけど却ってややこしくなるからそのまま
s'[2] ^= mat2 // 0xfc78ff1fだけど同上
}
基本事項の確認
この前の記事と同様に、整数を2進数表記して上のベクトルとして扱っていきます。
(最終的には内部状態を128次ベクトルとして次の状態へ移す行列を考えますが、
各statusごとに分割して処理が書かれているので、一度各statusごとの式に落とし込んでから128次ベクトルにまとめ上げていきます。)
このあたりはoupo先生の記事とかMTを作った松本眞氏の講義ノートとかを参考にしたので詳しくはそちらで。
○各statusやx,y等の32bit整数を32次横ベクトルとみなし、それぞれ,
等と表します。
○これにより、各処理は以下のように表すことができます。
・排他的論理和xor(^)
32bit整数a, bの排他的論理和を取る処理a^bは、に相当します。
・ビットシフト(<< n, >> n)
単位行列の対角上にある1を、左nビットシフトは左に、右nビットシフトは右にnずらした行列との積で表せます。
例) 11 << 2 (%16)
$$
\begin{align}
\begin{bmatrix}
1 & 0 & 1 & 1
\end{bmatrix}
\begin{bmatrix}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
\end{bmatrix}=
\begin{bmatrix}
1 & 1 & 0 & 0
\end{bmatrix}
\end{align}
$$
・論理積and(&)
a&bは、で表せます。言い換えると、aと対角上にbの各成分を並べた行列との積です。
例) 11 & 6
$$
\begin{align}
\begin{bmatrix}
1 & 0 & 1 & 1
\end{bmatrix}
\begin{bmatrix}
0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 \\
\end{bmatrix}=
\begin{bmatrix}
0 & 0 & 1 & 0
\end{bmatrix}
\end{align}
$$
・また、if(y&1==1) a^=bは、32列目にの各要素並べた行列
を用いて、
と表せます。
例) if(y&1) a^=11を表す行列
$$
A =
\begin{align}
\begin{bmatrix}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
1 & 0 & 1 & 1 \\
\end{bmatrix}
\end{align}
$$
さて、準備が整ったところで計算していきましょう。
1行目~4行目
・1行目 そのまんまです。
$$
{\boldsymbol y} = {\boldsymbol s}_3
$$
・2行目 に
& 0x7FFFFFFFに相当する行列を掛けます。
(の下位31bitを取るので、
と置きます。)
$$
\begin{align}
{\boldsymbol x}
& = {\boldsymbol s}_0
\begin{bmatrix}
0 & & & \\
& 1 & & \\
& & \ddots & \\
& & & 1
\end{bmatrix} +
{\boldsymbol s}_1 +
{\boldsymbol s}_2 \\
& = {\boldsymbol s}_0 U_{31} + {\boldsymbol s}_1 + {\boldsymbol s}_2
\end{align}
$$
・3行目 左辺と右辺で文字を変えるべきなのでしょうが、=を左辺への代入だと思ってください。。。
(以下、左nビットシフトを表す行列を、右nビットシフトを表す行列を
と置きます。)
$$
\begin{align}
{\boldsymbol x} &= {\boldsymbol x} + {\boldsymbol x} L_{1} \\
&= {\boldsymbol x} (I + L_{1}) \\
&= {\boldsymbol s}_{0}U_{31} (I+L_{1}) + {\boldsymbol s}_{1}(I+L_{1}) + {\boldsymbol s}_{2} (I+L_{1})
\end{align}
$$
・4行目
$$
\begin{align}
{\boldsymbol y} &= {\boldsymbol y} + {\boldsymbol y} R_{1} + {\boldsymbol x} \\
&= {\boldsymbol y} (I + R_{1}) + {\boldsymbol x} \\
&= {\boldsymbol s}_{0}U_{31} (I+L_{1}) + {\boldsymbol s}_{1}(I+L_{1}) + {\boldsymbol s}_{2} (I+L_{1}) + {\boldsymbol s}_{3} (I + R_{1})
\end{align}
$$
これでが出ました。
次はこれらをstatusへ代入していきます。
5行目以降
更新後のstatusをとします。
・5, 6行目 ただ代入するだけです。
$$
\begin{align}
{\boldsymbol s}'_{0} = {\boldsymbol s}_{1} \\
{\boldsymbol s}'_{1} = {\boldsymbol s}_{2}
\end{align}
$$
・7行目 ちょっと長ったらしくなります。見やすくするために,
と置きます。
$$
\begin{align}
{\boldsymbol s}'_{2} &= {\boldsymbol x} + {\boldsymbol y}L_{10} \\
&= {\boldsymbol s}_{0}U_{31} (I+L_{1}) + {\boldsymbol s}_{1}(I+L_{1}) + {\boldsymbol s}_{2} (I+L_{1}) \\
&\quad + ({\boldsymbol s}_{0}U_{31} (I+L_{1}) + {\boldsymbol s}_{1}(I+L_{1}) + {\boldsymbol s}_{2} (I+L_{1}) + {\boldsymbol s}_{3} (I + R_{1}))L_{10} \\
&= {\boldsymbol s}_{0}U_{31}L'_{1}L'_{10} + {\boldsymbol s}_{1}L'_{1}L'_{10} + {\boldsymbol s}_{2}L'_{1}L'_{10} + {\boldsymbol s}_{3}R'_{1}L_{10}
\end{align}
$$
・8行目
を代入するだけです。
$$
\begin{align}
{\boldsymbol s}'_{3} = {\boldsymbol s}_{0}U_{31} L'_{1} + {\boldsymbol s}_{1}L'_{1} + {\boldsymbol s}_{2} L'_{1} + {\boldsymbol s}_{3} R'_{1}
\end{align}
$$
・
if内の処理
if(y&1) s[1] ^= mat1を表す行列を、
if(y&1) s[2] ^= mat2を表す行列をと置きます。
を作用させると最下位bitは必ず0になるので、
(よって
)が成り立つことに注意します。
$$
\begin{align}
{\boldsymbol s}'_{1} &= {s}'_{1} + {\boldsymbol y}C_{mat1} \\
&= {\boldsymbol s}_{2} + ({\boldsymbol s}_{0}U_{31} L'_{1} + {\boldsymbol s}_{1}L'_{1} + {\boldsymbol s}_{2} L'_{1} + {\boldsymbol s}_{3} R'_{1})C_{mat1} \\
&= {\boldsymbol s}_{0}U_{31} L'_{1}C_{mat1} + {\boldsymbol s}_{1}L'_{1}C_{mat1} + {\boldsymbol s}_{2} (I+L'_{1}C_{mat1}) + {\boldsymbol s}_{3} R'_{1}C_{mat1} \\
&= {\boldsymbol s}_{0}U_{31} C_{mat1} + {\boldsymbol s}_{1}C_{mat1} + {\boldsymbol s}_{2} (I+C_{mat1}) + {\boldsymbol s}_{3} (I + R_{1})C_{mat1}
\end{align}
$$
$$
\begin{align}
{\boldsymbol s}'_{2} &= {\boldsymbol s}'_{2} + {\boldsymbol y}C_{mat2} \\
&= ({\boldsymbol s}_{0}U_{31}L'_{1}L'_{10} + {\boldsymbol s}_{1}L'_{1}L'_{10} + {\boldsymbol s}_{2}L'_{1}L'_{10} + {\boldsymbol s}_{3}R'_{1}L'_{10}) +({\boldsymbol s}_{0}U_{31} L'_{1} + {\boldsymbol s}_{1}L'_{1} + {\boldsymbol s}_{2} L'_{1} + {\boldsymbol s}_{3} R'_{1})C_{mat2} \\
&= {\boldsymbol s}_{0}U_{31}(L'_{1}L'_{10} + C_{mat2}) + {\boldsymbol s}_{1}(L'_{1}L'_{10} + C_{mat2}) + {\boldsymbol s}_{2}(L'_{1}L'_{10} + C_{mat2}) + {\boldsymbol s}_{3}(R'_{1}L_{10} + R'_{1}C_{mat2})
\end{align}
$$
整理してみる。
何とか処理を式に落とし込むことができたので、行列にしやすいように整理してみます。
$$
{\boldsymbol s}'_{0} = {\boldsymbol s}_{0} {\boldsymbol O} + {\boldsymbol s}_{1} + {\boldsymbol s}_{2}{\boldsymbol O}+ {\boldsymbol s}_{3}{\boldsymbol O} \\
{\boldsymbol s}'_{1} = {\boldsymbol s}_{0}U_{31} C_{mat1} + {\boldsymbol s}_{1}C_{mat1} + {\boldsymbol s}_{2} (I+C_{mat1}) + {\boldsymbol s}_{3} (I + R_{1})C_{mat1} \\
{\boldsymbol s}'_{2} = {\boldsymbol s}_{0}U_{31}(L'_{1}L'_{10} + C_{mat2}) + {\boldsymbol s}_{1}(L'_{1}L'_{10} + C_{mat2}) + {\boldsymbol s}_{2}(L'_{1}L'_{10} + C_{mat2}) + {\boldsymbol s}_{3}(R'_{1}L_{10} + R'_{1}C_{mat2}) \\
{\boldsymbol s}'_{3} = {\boldsymbol s}_{0}U_{31} L'_{1} + {\boldsymbol s}_{1}L'_{1} + {\boldsymbol s}_{2} L'_{1} + {\boldsymbol s}_{3} R'_{1}
$$
さて、これで各と
を並べたベクトルをそれぞれ作り、内部状態の更新を行列で表現すると
$$
\begin{align}
\begin{bmatrix}
{\boldsymbol s}'_{0} & {\boldsymbol s}'_{1} & {\boldsymbol s}'_{2} & {\boldsymbol s}'_{3}
\end{bmatrix} =
\begin{bmatrix}
{\boldsymbol s}_{0} & {\boldsymbol s}_{1} & {\boldsymbol s}_{2} & {\boldsymbol s}_{3}
\end{bmatrix}
\begin{bmatrix}
{\boldsymbol O} & U_{31}C_{mat1} & U_{31}(L'_{1}L'_{10}+ C_{mat2}) & U_{31} L'_{1} \\
I & C_{mat1} & L'_{1}L'_{10} + C_{mat2} & L'_{1} \\
{\boldsymbol O} & I+C_{mat1} & L'_{1}L'_{10} + C_{mat2} & L'_{1} \\
{\boldsymbol O} & (I + R_{1})C_{mat1} & R'_{1}L_{10} + R'_{1}C_{mat2} & R'_{1}
\end{bmatrix}
\end{align}
$$
となることがわかりました。
あとはこの行列を具体的に{0, 1}で表すだけですね!
後編に続く!!! →TinyMTの更新を行列で書いてみようのコーナー(後編) - yatsuna_827’s blog
